DESとは?
今日は暗号のお話です。DES暗号について調べてみました!
DESは暗号の方式(アルゴリズム)を広く公開した商用の暗号です。
暗号はそれまでは軍事用として使われていました。
そのため、誰がどのような暗号を使用しているか、アルゴリズム自体もトップシークレットでした。
しかし戦後、コンピュータを多くの人が使うようになると、
企業間での商取引等、インターネット上でやり取りするデータの暗号化が必要となりました。
しかし、異なる企業間でやり取りをする際、お互いが別々の暗号方式を使っていては
情報のやりとりができません。そこで、IBMのHorst Feistelによって、
「鍵」を秘密にし、「暗号アルゴリズム」は公開するDESが、
暗号モジュールに関するセキュリティ要件の仕様を規定する米国連邦
標準規格(FIPS 140)に採用されました。
では、DESの仕組みを見てみましょう!
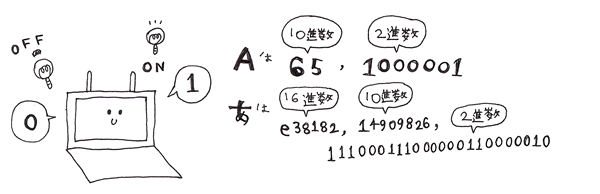
コンピュータでは、電気が通っていない状態を「0」、通っている状態を「1」とする
2進数で情報を置き換えてやり取りしています。
なのでDESによる暗号化でも2進数に変換して考えます。
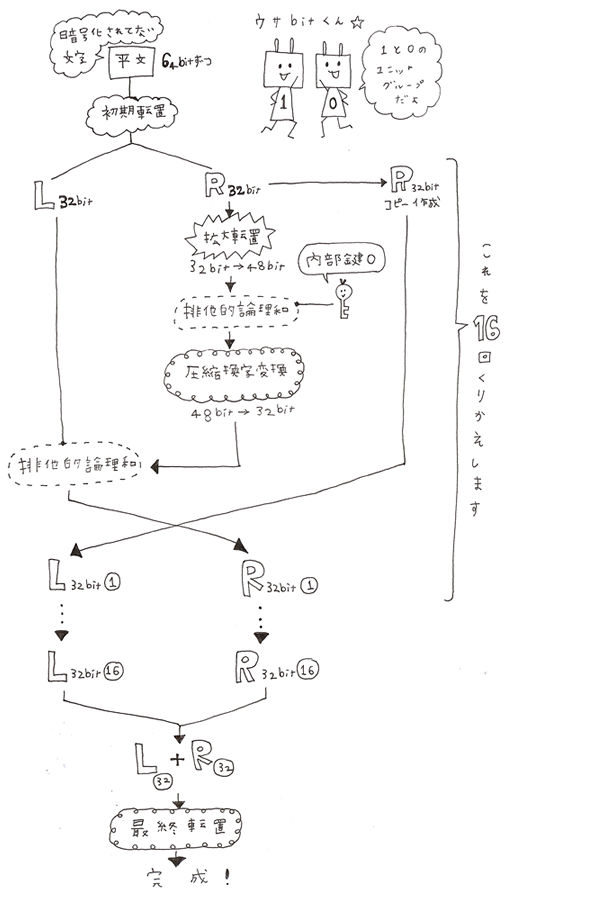
DESの暗号化の流れはこのようになっています。
では、実際に暗号化の様子を見てみましょう!
まず、暗号化されていない文章(平文)を2進数にして64bitごとにブロック化します。
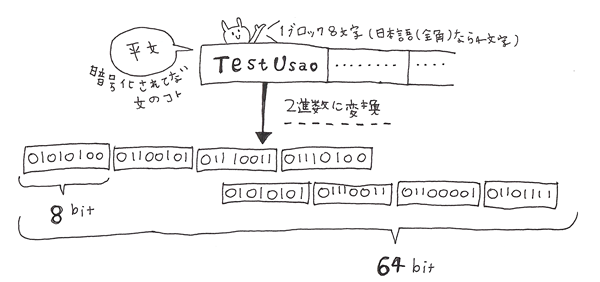
英数字なら1ブロック8文字、全角日本語なら1ブロック4文字となります。
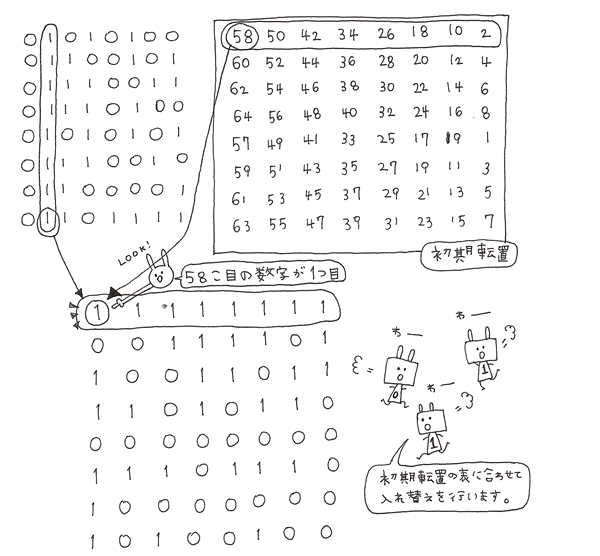
そのブロックを「初期転置」と呼ばれるbitの入れ替えを行います。
DESでは暗号アルゴリズムが公開されているので、どのように入れ替えるかも公開されおり、
表の番号順に並び替えを行います。
先ほど64bitごとに区切りましたが、58bit目が1文字目、50bit目が2文字目…と並び替えます。
よく見ると縦の列を横の列に並び替えているのがわかります。
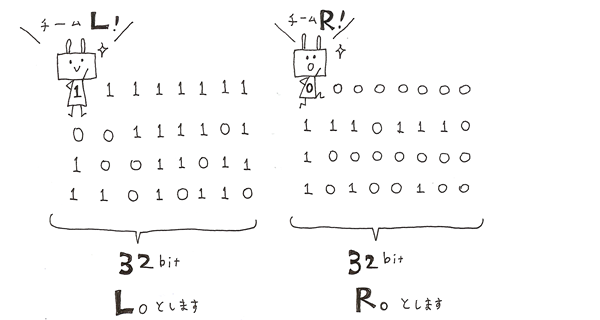
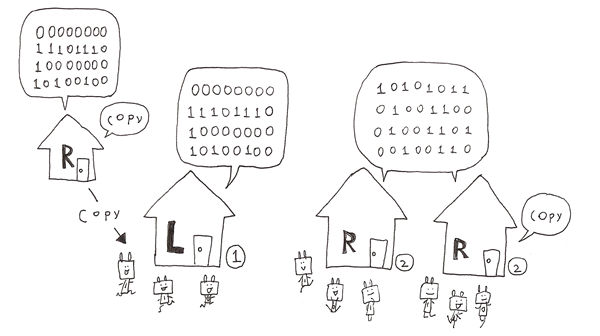
入れ替えたものを32bitずつ、LとRに2つに分けます。
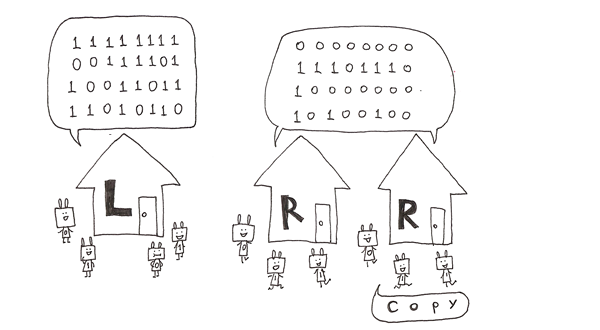
ここで、Rのコピーを作ります。
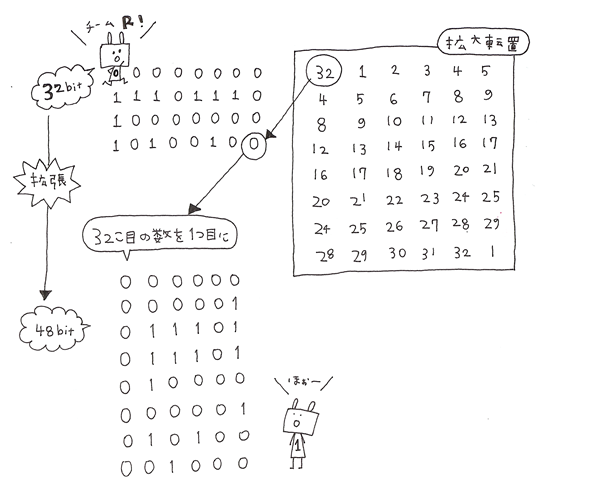
次に、Rの方だけに拡大型転置を行い再び入れ替えを行います。
初期転置の表と同じく拡大転置の表も公開されています。
32bit目が1文字目、1bit目が2文字目です。
列の5・6bit目と次の列の1・2bit目の数字が同じになるようになっていて、
入れ替えると32bitから48bitに増えるようになっているので「拡大」転置です。
拡大型転置を行ったRと作成した内部鍵で排他的論理和をとります。
…排他的論理和とは?
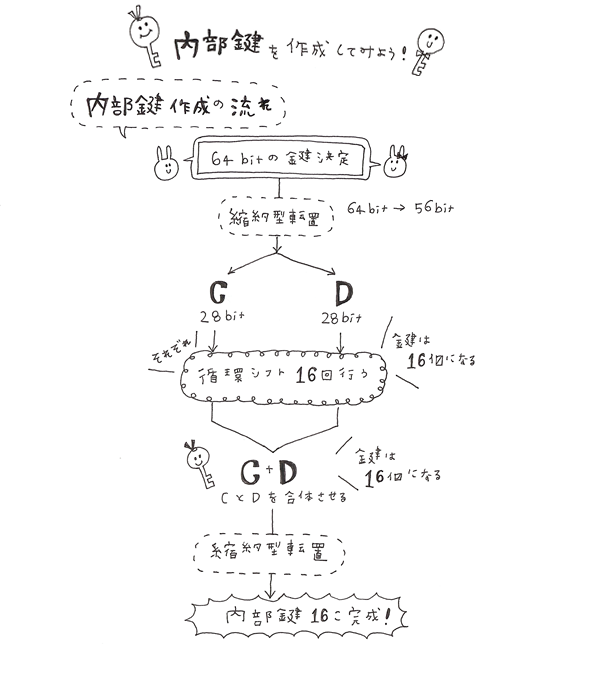
その前にまず、内部鍵を作成しましょう!
DESの流れの絵でも書いた通り、DESでは16回内部鍵との排他的論理和をとるため、
内部鍵も16個作成します。
DESは共通鍵暗号方式の1つです。
暗号をやり取りするもの同士で共通の鍵を持って暗号化・複合を行います。
まず、データをやりとりするもの同士で56bitの鍵を決めます。
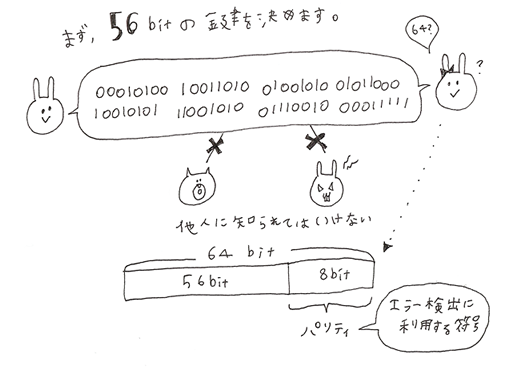
この時の鍵は56bit+エラー検出に利用する符号パリティ8bitで64bitになっています。
「暗号アルゴリズム」を公開するかわりに「鍵」は秘密になっているため、
鍵は誰にも知られずにやりとりをする必要があります。
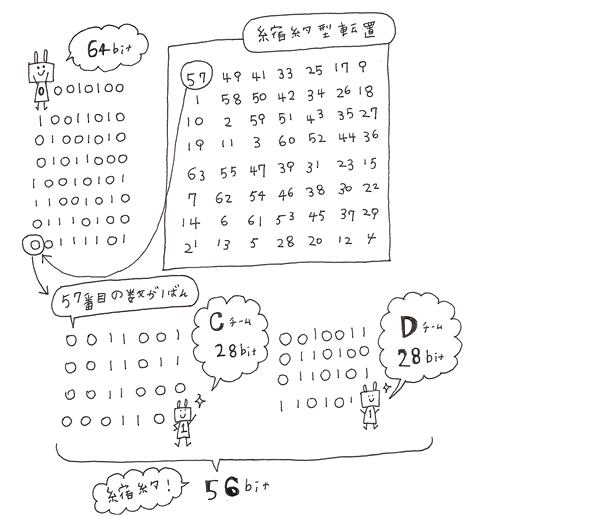
そのデータに縮約型転置を行います。
転置前は64bitで57bit目を1文字目に、49bit目を2文字目に入れ替えを行います。
入れ替えが行われると64bitから56bitに縮約され、これを28bitずつ左右に分けてそれぞれCとDとします。
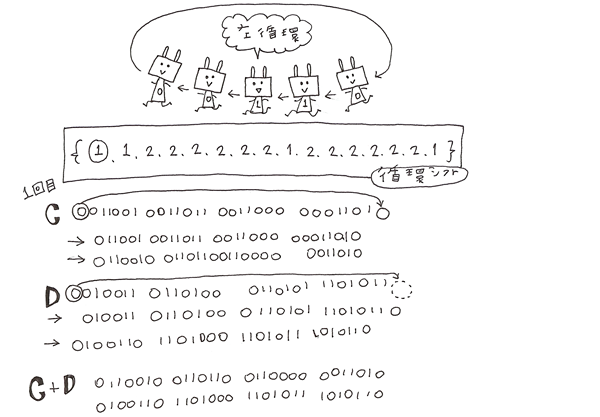
次に循環シフトを行います。
1番前の数字を順番に一番後ろに移動させるので循環シフトです。
循環シフトの表には、どれだけ循環させるのかが書かれています。
16個の鍵を作るので表の数字は16個ありますね。
1つ目の鍵の時は1のようなので1文字目だけ後ろに循環させます。
CとD、それぞれに循環シフトを行った後CとDを合体させ、
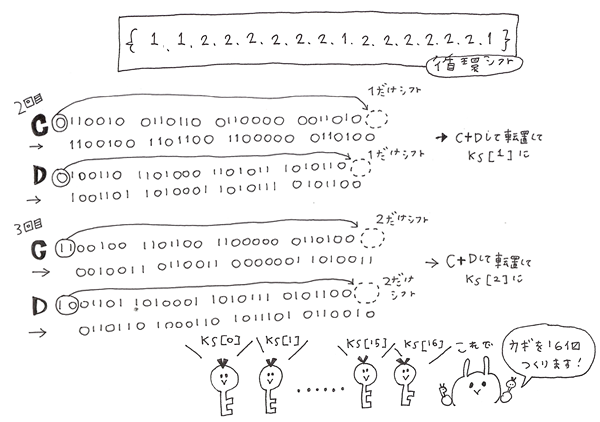
縮約型転置を行って、入れ替えて48bitにします。
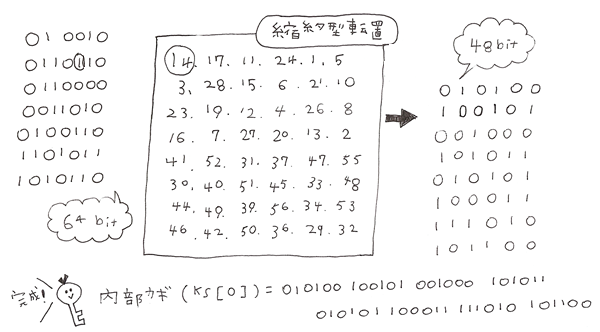
同じように2回目、3回目と循環シフトを行い、
それぞれに縮約型転置を行って1つの鍵から16個の内部鍵を作ります。
これで内部鍵が完成です!
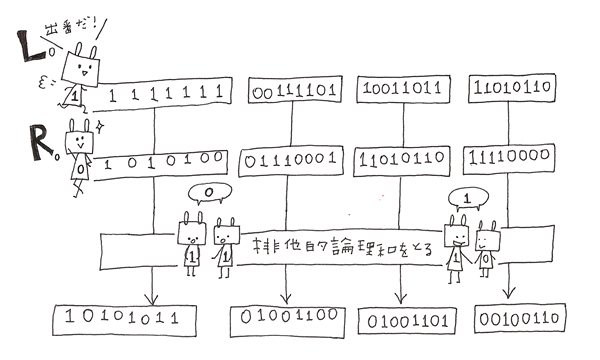
では、拡大型転置を行ったRと内部鍵で排他的論理和をとりましょう。
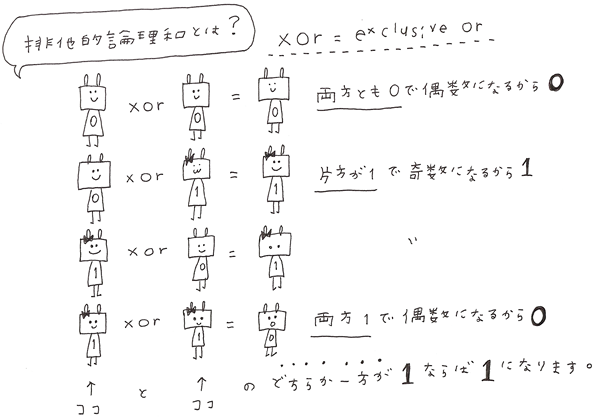
排他的論理和とは、1と1なら0、0と1なら1、0と0なら0というように、
どちらか一方が1ならば1を、それ以外(どちらも1、どちらも0)なら0を返す論理演算のことをいいます。
「どちらか一方が1」なら1です。
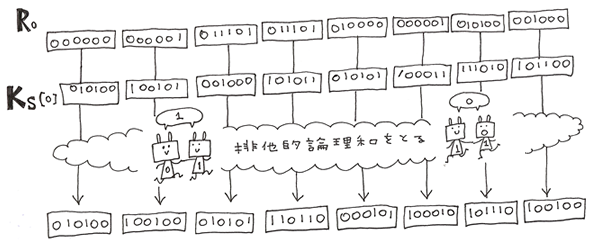
Rと内部鍵の1つ目で排他的論理和をとります。
排他的論理和をとったRを6bitごとに8つにわけます。
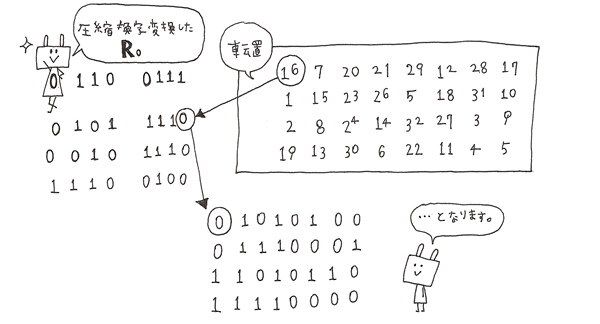
今度は圧縮換字変換Sに基づいて圧縮換字変換というものを行います。
6bitを4bitに圧縮。表から代替する数字を選び換字変換します。
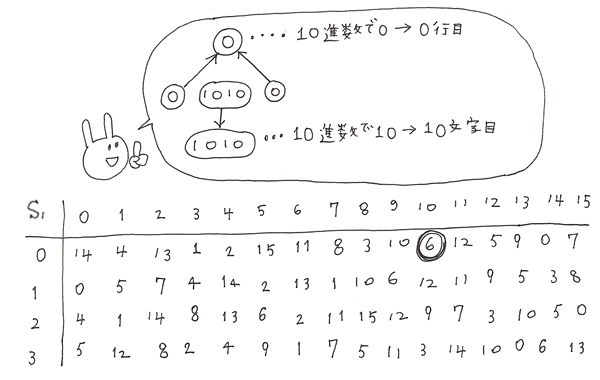
表はこのように8つあります。これを8つにわけた6bitにそれぞれ使用します。
まず、1bit目と6bit目を合体させて行数を選びます。
この場合、0と0なので0。2進数の0は10進数でも0なので0行目になります。
次に、真ん中の4bitを使って何文字目かを決めます。
この場合、2進数の1010は10進数では10になるので10文字目。
なので0行目の10文字目を選びます。
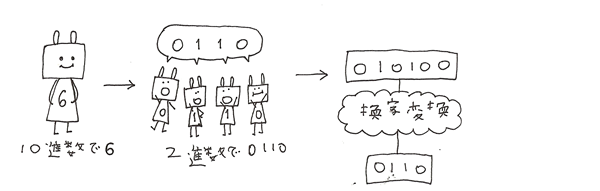
ここでは6になるので、10進数で6は2進数では0110となるので、010100は0110に換字変換されます。
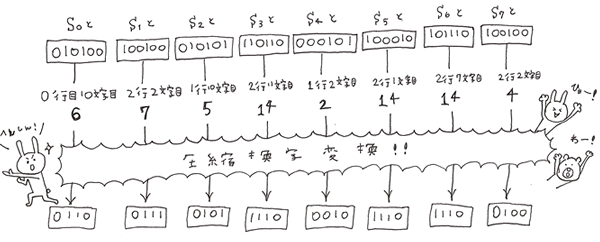
おなじようにそれぞれ8つの6bitを4bitに換字変換していきます。
次に再び転置を行い、
ここで最初に分けたLとこれまでの作業を行ったRの排他的論理和をとります。
ここで、最初のRをコピーしたものをL1、Lと排他的論理和をとったものをR1として1回目は終了です。
同じように2回目、3回目…とL16、R16になるまで16回繰り返します。
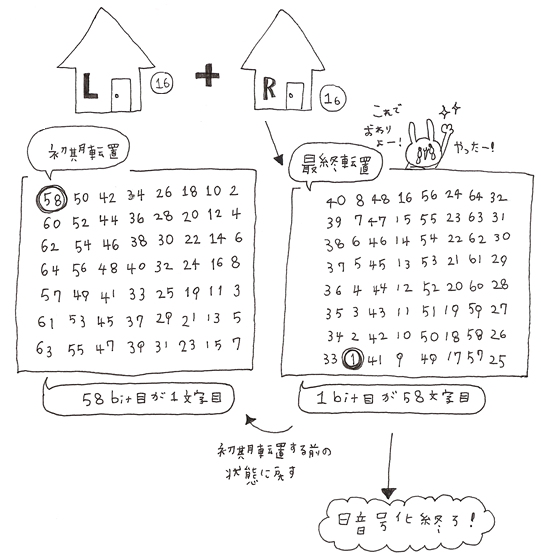
いよいよL16、R16となったらLとRを合体させて最終転置を行います。
最終転置の表は、初期転置で行ったものと反対になっているのがわかります。
最終転置ができたら暗号化終了です!


Comments: 0