ECC版SSL証明書インストール体験記その1
実は小悪魔ブログ、ECC対応版SSLサーバ証明書の導入を行いました。
商用での導入は小悪魔ブログとディレクターズのkmonos.jpが世界初!なのです〜(どんどんぱふぱふ〜!)
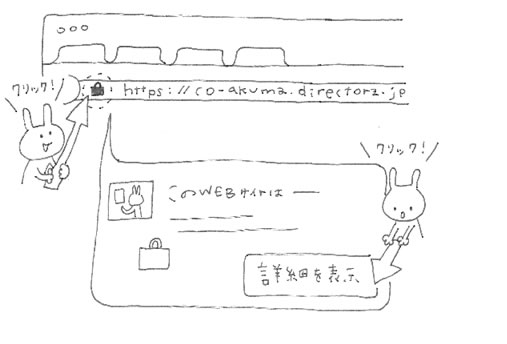
ではみなさん…小悪魔ブログのURLの鍵マークを押して♪
詳細を表示を押してみてっ♪
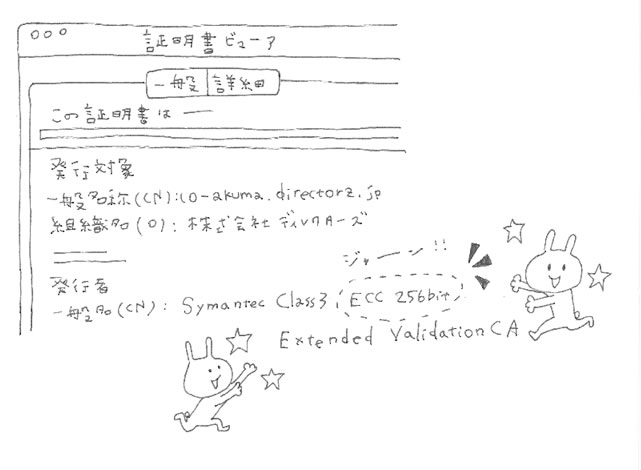
ECCと書かれているのを確認して頂けましたでしょうかー!(どやっ)
しかし…
導入までは山有り谷有りありました…
今日はECC対応版SSLサーバ証明書の導入体験日記ですっ
ところでECC対応版SSLサーバ証明書とは????
これまでのRSA版SSLサーバ証明書とはどう違うのでしょう?
RSA暗号はマサチューセッツ工科大学の3人の研究者によって開発されました。
「RSA」という名前はその3人の頭文字から名付けられています。
RSA暗号の世界はちょっぴり特殊で、「ある数までいくと0に戻る世界」を使用します。
んん?なにその世界?となった方も多いと思いますが、
例えば時計。
時計は12時は0時、13時は1時…と
12までいくと0に戻る世界を利用していますよね。
また、12まで行くと0に戻るということは、
12で割った数の「余り」を計算するのと同じことにもなります。
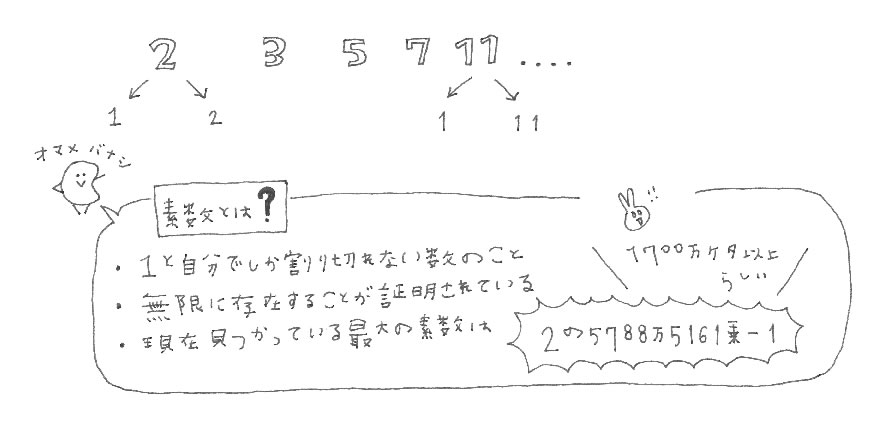
RSAでは、鍵を作る時に2つの素数を使用します。
素数とは1と自分でしか割り切ることのできない数のこと。
RSAでは2つの素数を用いてワンペアの公開鍵・秘密鍵を作ります。
「2つの素数を掛けた数」が公開鍵の一部として公開されますが、
鍵のもととなる2つの素数は公開せず隠します。
鍵の作り方は後日紹介する(かも?)として…
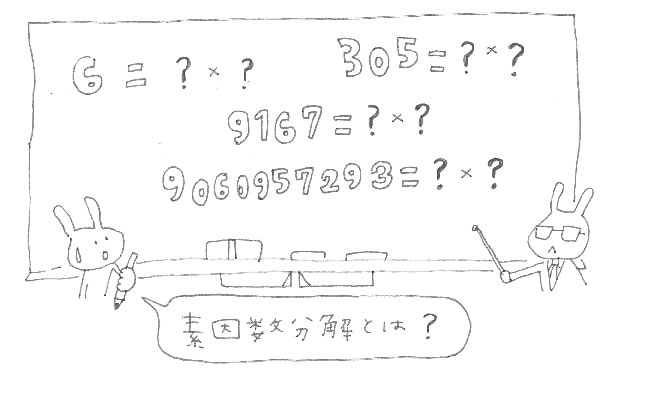
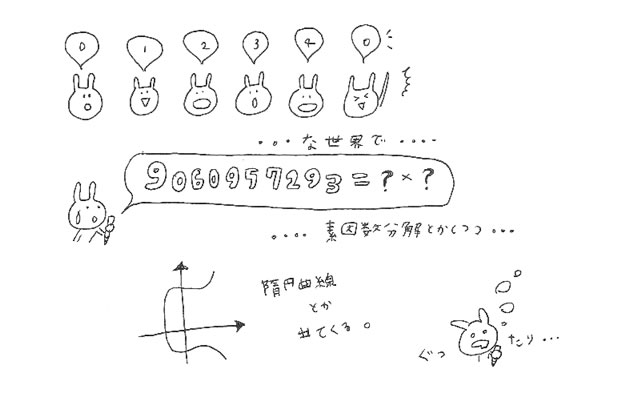
RSA暗号の解読の難しさは「素因数分解の難しさ」に由来します。
ある数を2つの素数に分けることを素因数分解といいます。
実は、効率的に素因数分解する方法はまだ見つかっていないのです。
RSA暗号では公開鍵から秘密鍵を見つけようとすると、
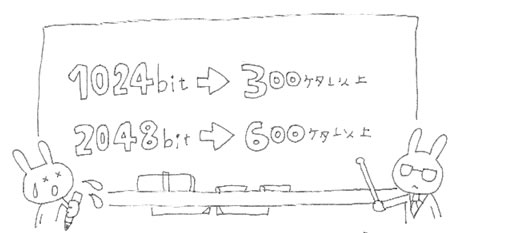
2つの素数を掛けた数である600桁以上(2048bit)の数を素因数分解し、
公開鍵・秘密鍵を作る為に使った2つの素数を割り出す必要があります。
コンピュータを使えば簡単に素因数分解できるのでは?と思ってしまいますが、
現在、素因数分解に成功している世界記録の数は232桁(768bit)。
さらに鍵を長くすれば長くするほど素因数分解は難しくなり暗号化強度も増していきます。
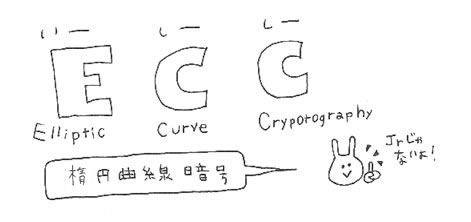
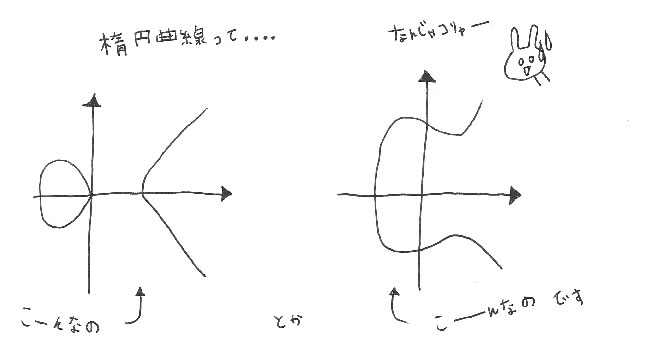
ECC暗号は楕円曲線と呼ばれる数式を使った公開鍵暗号方式です。
楕円曲線暗号の仕組みについては文系の小悪魔にはすっごーーーーーーーーーーーーーーーーーーーーーく難しいのですが、
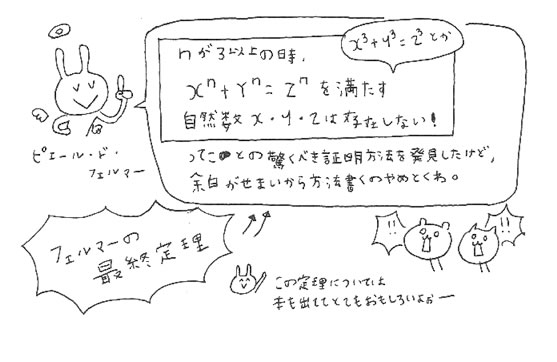
楕円曲線暗号は世界の数学史上最大の難問と呼ばれている「フェルマーの最終定理」を解く鍵にもなったりもしています。
RSAは768bitを解読するのに300台のPCで3年かかったものの、
少しずつ解読を効率的に行なう手法が発見されつつありますが、
楕円曲線暗号は未だ効率的に解析するアルゴリズムは存在していません。
そのため、より短い鍵長での暗号化をすることが可能となり、
RSAの1024bitとECCの160bitはほぼ同等の暗号化強度を持っています。




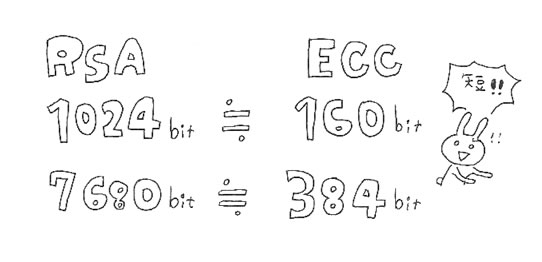
Comments: 0